パンを分けるには？ - おきなのささやき

３個のパンを５人に分ける方法。１回で、１切断面で分けれるのか？

面白い話をWebで読んだ。「人間がつくった最初の数」伊藤文治^ଅ）．

分数の起こりについての話だが、興味のある部分だけ抜き出した。ご容赦（詳しくはweb）。

TP: 三つのパンを5人で等分に分けるとき、どのように分けたらよいかという問題である。古代エジプト人は１より小さいあらゆる大きさを異なる単位分数（分子が１）の和で表されていた（注：エジプトの分数には分子がない^ឆ））。例えば、２/５＝１/３＋１/１５、２/７＝１/４＋１/２８のように。１/Ｘ＋１/Ｙにして考える。また剰余計算は２倍、10倍だけで行われたようである。さて、現代人の多くは三つとも１つのパンを5等分（３/５）に切って分配するのではと思われる。しかし、古代エジプト人は、２と１０、すなわち１/２＋１/１０（エジプト式の記載は、^/２^/10：斜線/はー）を用いたと著者は推測している。古代エジプト人はできるだけ大きなピース（単位分数）を一つ目と考え、最初にパンを三つとも半分（１/２）に切って５人に配る（半分は６つになるから、半分１つ余る）。残りの半分１つを５等分（１/２×１/５=1/10）して分ける。なるほど、面白い。興味ある方は下記文献ឆ）を。

大事なのはここからである。パンを切る回数である。三つのパンをそれぞれ５等分して各人に配るのには、３×４＝１２回パンを切る必要がでてくる。これに対して古代エジプト人は最初に一つを半分に切ったパン６個（三つを１/２カットする）のうち５個を各人に配り、残り半分の１個を５つに切って配る。すなわち、パンを切る回数は６回（３＋３）で済む、とある。私は数学者でないので、1個のパンを３回の切断で均等に５個に分ける方法をすぐ思いつかなかったが、結構難しいか（３+４なら簡単だが）。もし、３回の切断で５個に分けるというのであれば、三つのパンをそれぞれ切って分ける回数は３×３＝９回となる。これはさておき、古代エジプト人にとって必要なのは、切る回数を少なくすることだったと結論している。普通はふうん、とか、そうだったんだで終わってしまう。・・・・しかし、拙者（おきな）は違う。以下、暇があれば。

１回で５個に切り分ける方法を考えてみよう。古代エジプト人はもっと別な方法を考えたのでは？アレクサンドリア図書館のパピルスに書かれていたことを想像しよう。例えば、３枚のパンを重ねて半分に切ると１回、残り半分のパンを５個に切ると３回、合計４回で済むことになる。次にもっと切る回数を減らすことできないかと思案すると、パンを折り曲げることを思いつく。３枚のパンを重ねて、一番上のパンを折り曲げて（図１では４回曲げる）切ると、１回で３個のパンを半分（１/２）と残り１/５（全体の２０％）を分けることができる。この場合のパンの切断面は７である。　

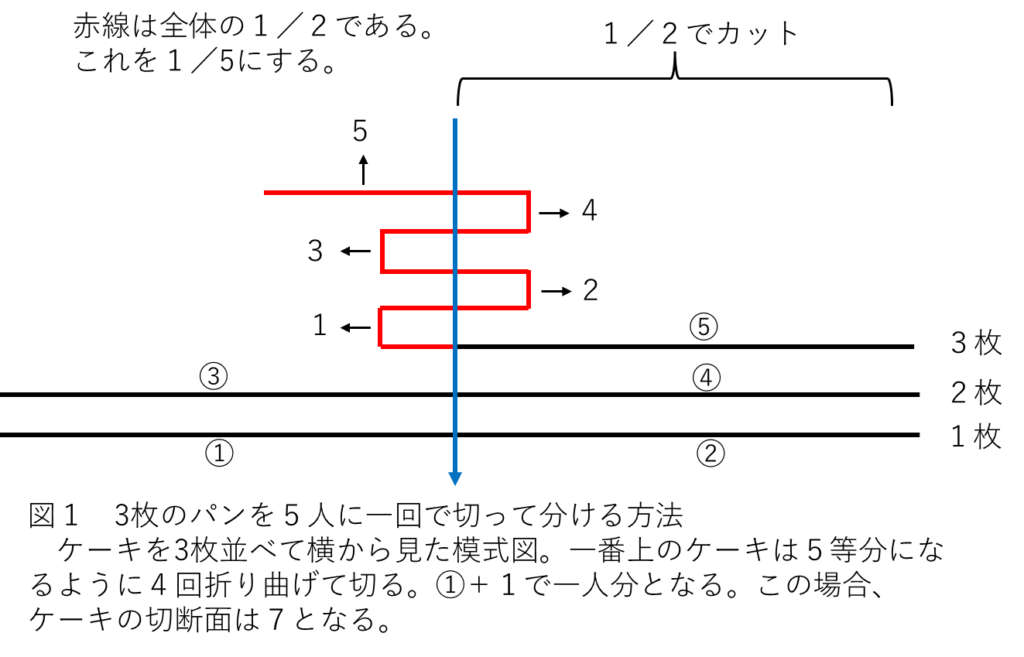
さらに合理的に考えると、3枚のパンを重ねて、一番上のパンを折り曲げて（図２では３回曲げる）切ると、1回で２個のパンを半分（１/２）、1個のパン（３枚目）は半分と１/５をつなげたものと残り１/５（全体の20％）を切り分けることができる。また、パンの切断面は６で済む。ただし、ここでは、パンの形はくびれや歪みがなく閉じられていて、重さ（質量）、形が同一で、すぐには崩壊しないパンであることを前提としてる。もちろん、五つのパンを分け与えていくとみんなにいきわたるパンではない。パンというと勝手に丸いパン、角食パンを想像してしまうが、先入観に注意が必要である。

１回のカットで、１つの断面で　ここで終わっては「ささやき」にならない。３個のパンを１回で、しかも１つの断面で５つに切り分けることはできないのか？普通に考えると、おきなの頭では無理なので反則的なことを考える。あくまで、ユークリッド幾何学の中で、直線で切る場合を想定する。当然ながら包丁の刃も1枚である。１回のカットで、しかも１つの断面で３つに分けることができる方法が見つかれば５つに分けるのも同じことであるので、３つに分けることを考えてみる。

結合パン　ここで、デフォルメしたパンを考えることにする。つまり、何でもありなパンを想像（創造）してもらいたい。１回で３つに切り分けることはできるが（図３a のようにパンを折り曲げるなど）、２つの切断面が生じる。「１つの断面しかもたない」ことが重要なポイントである。例えば、１か所の点でつながっているようなパンは、接続点を切っても１つの断面のみで３つにはならない（図３b）。あるいは、図３c のようになっていても３つにはならない。ただし、接点に関しては、分子レベルでの化学結合については考えないこととする。無理にプラトンのイディア（線分の比喩、洞窟の比喩）の話^δ)をもち出すまでもない。

リングパン　そこで、編み出されたのは、輪である。リングとなっているパンをリング1か所を切断すると分かれる仕組みである。図４a.は、２つのパンは一か所欠けた輪でつながっていて、固定している。一つのパンはその輪の中で動くことができる。同じ長さの箇所で輪を切ることで3つの同じパンに分けることができる。また、図４b.はaをデフォルメしただけであるが、２つの輪のパンがつながっていて、１つのパンがそのつながっている棒状の中を移動できる。棒状のパンの１箇所を切断すると３つの同じパンに分けることができる。当然であるが、３つに分かれたパンの形と重量は同じであるとする。すでにパンが分かれているのではないかとの批判があるだろうが、ひとつのパンとみなしてほしい（位相幾何学については全く無知である。能力の限界）。

タマゴパン　図５のように球の中にパンが入っている場合、1回のカットにより１切断面で３つのパンを生み出せる。図５aでは球のパンの中にそれと結合していない半分のパンが片側にある。このパンを半分に切った場合、切られた半球の２つのパンと中に入っていた半球のパンができる。図５bは球のパンに２つの空洞のパン（空洞でなくてもよい）が入っていて、全体のパンとは結合していない。この場合、球の全体を切らずに中の２つを取り出すと、３つのパンができる。形状は異なるが、３つに分かれたパンの重量は同じとする。

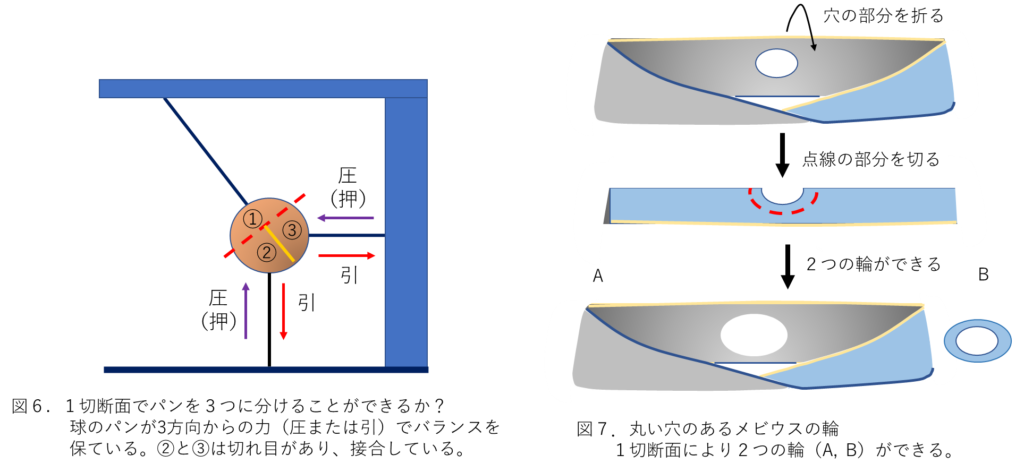
重力バランスパン　図６は、球のパンが３方向からの力（圧または引）でバランスが保たれている。②と③は切れ目があり、接している。①下の点線の部分できることにより3方向のbランスが崩れてそれぞれ分離する。これも1回で1切断面で３つのパンに分かれる例であろう。　　　　　　　　　　　　

メビウスの輪パン—これはいままでの話とは異なる。メビウスの輪を切ると二つに分かれずに一つの大きな輪になると思っているのではないだろうか。これは、あくまで輪の中を切り進んで１周させたときである。当然ながら、輪の横を切るとひもになる（両端ができる）。しかし、ねじれの個所を折りたたんで輪に沿って半分に切ると二つに分かれる。普通の輪とメビウスの輪は位相空間（トーラス）としては同相であるからか？別々の二つの輪になるように切れたことがないので、試していただきたい。ただし、図７に示したように、輪の中を丸く切り抜き、折り曲げてその周囲を切り取るとメビウスの輪の本体の切り抜いた輪の二つができる。もちろん、３つの輪も作ることができる。輪の中に２つの穴を作って穴を合わせて折り曲げて切ると、本体と２つの輪ができる。メビウスの輪を切ると、１つの輪ができるだけではないのである。ちなみにメビウスの輪を一つの輪となるように一太刀で切ることのできる「メビウスの輪カット専用ハサミ」も考案したが。暇ならば作ってみてはどうか。